Teoría de la decisión estadística, ensayos de hipótesis y significación (página 2)
En la práctica se acostumbra a utilizar niveles
de significación del 0.05 ó 0.01, aunque igualmente
pueden emplearse otros valores. Si,
por ejemplo, se elige un nivel de significación del 0.05
ó 5 % al diseñar un ensayo de
hipótesis, entonces hay aproximadamente 5
ocasiones en 100 en que se rechazaría la
hipótesis cuando
debería ser aceptada, es decir, se está con un 95 %
de confianza de que se toma la decisión adecuada.
En tal caso se dice que la hipótesis ha sido rechazada
al nivel de significación del 0.05, lo que significa
que se puede cometer error con una probabilidad
de 0.05.
Ensayos
referentes a la distribución normal
Para aclarar las ideas anteriores, supóngase que
con una hipótesis dada, la distribución muestral de un
estadístico S es una distribución normal con media
µs Y desviación típica uso
Entonces la distribución de la variable tipificada
(representada por z) dada por z = (S
–µs) /ss, es una normal tipificada (media 0,
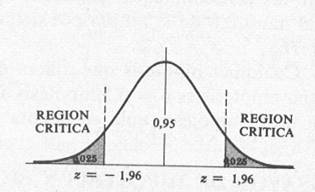
varianza 1) y se muestra en la
figura.
Como se indica en la figura, se puede estar con el 95 %
de confianza de que, si la hipótesis es cierta, el
valor de
z obtenido de una muestra real para el
estadístico S se encontrará entre -1.96 y 1.96
(puesto que el área bajo la curva normal entre estos
valores es 0.95).
Sin embargo, si al elegir una muestra al azar se
encuentra que z para ese estadístico se halla
fuera del rango -1.96 a 1.96, lo que quiere decir que es
un suceso con probabilidad de solamente 0.05 (área
sombreada de la figura) si la hipótesis fuese verdadera.
Entonces puede decirse que esta z difiere
significativamente de la que cabía esperar bajo
esta hipótesis y se estaría inclinado a rechazar la
hipótesis.
El área total sombreada 0.05 es el nivel de
significación del ensayo.
Representa la probabilidad de cometer error al rechazar la
hipótesis es decir, la probabilidad de cometer error del
Tipo I. Así, pues, se dice que la hipótesis se
rechaza al nivel de significación del 0.05 o que
la z obtenida del estadístico muestral dado es
significativa al nivel de significación del
0.05.
El conjunto de las z que se encuentran fuera
del rango -1.96 a 1.96 constituyen lo que se llama
región crítica o región de rechace
de la hipótesis o región de
significación. El conjunto de las z que se
encuentran dentro del rango -1,96 a 1,96 podía entonces
llamarse región de aceptación de la
hipótesis o región de no
significación.
De acuerdo con lo dicho hasta ahora; se puede formular
la siguiente regla de decisión o ensayo de
hipótesis o significación.
(a) Se rechaza la hipótesis al nivel de
significación del 0.05 si la z obtenida para el
estadístico S se encuentra fuera del rango -1.96 a 1.96
(es decir, z > 1,96 o z < -1,96). Esto
equivale a decir que el estadístico muestral observado es
significativo al nivel del 0,05.
(b) Se acepta la hipótesis (o si se
desea no se toma decisión alguna) en caso
contrario.
A causa de su importante papel en los ensayos de
hipótesis y significación, z recibe
también el nombre de ensayo
estadístico.

Debe ponerse de manifiesto que pueden
igualmente emplearse otros niveles de significación. Por
ejemplo, si se utilizase el nivel del 0.01 se sustituiría
1.96 en todo lo visto anteriormente por 2.58 (véase
Tabla).
Ensayos de una y
dos colas
En el ensayo
anterior se atendía a los valores
extremos del estadístico S o su correspondiente z
a ambos lados de la media, es decir, en las dos
«colas» de la distribución. Por esta
razón, tales ensayos se llaman ensayos de dos
colas o ensayos bilaterales.
Sin embargo, con frecuencia, se puede estar solamente
interesado en los valores extremos a un solo lado de la media, es
decir, en una «cola» de la distribución, como,
por ejemplo, cuando se están ensayando la hipótesis
de que un proceso es
mejor que otro (que es diferente a ensayar si un proceso es mejor
o peor que otro). Tales ensayos se llaman ensayos de una
cola o ensayos unilaterales. En tales casos, la
región crítica es una región a un lado de la
distribución, con área igual al nivel de
significación.
La Tabla anterior, que da los valores críticos de
z para ensayos de una y dos colas a distintos niveles de
significación, será de utilidad para
propósitos de referencia. Valores críticos de
z para otros niveles de significación, se pueden
encontrar utilizando la tabla que da las áreas bajo la
curva normal.
Ensayos
especiales
Para muestras grandes, las distribuciones muestrales de
muchos estadísticos son distribuciones normales (o al
menos casi normales) con media µs y
desviación típica ss. En tales casos, se
pueden utilizar los resultados anteriores para formular reglas de
decisión o ensayos de hipótesis y
significación. Los siguientes casos especiales, son
solamente unos pocos de los estadísticos de interés
práctico. En cada caso, los resultados son para
poblaciones infinitas o para muestreo con
reemplazo. Para muestreo sin reemplazo de poblaciones finitas los
resultados deberán modificarse.
l. Medias. Aquí S = x, la media
muestral; µs = µx =
µ, media poblacional; ss = sx =
s/vN, donde µ es la desviación
típica poblacional y N es el tamaño de la
muestra. El valor de z viene dado por

Donde se utiliza la desviación muestral s o
S para estimar s.
2. Proporciones. Aquí S = P, la
proporción de «éxitos» en una muestra;
µ s = µ p = p, donde
p es la proporción de éxitos en la
población y N es el tamaño
de la muestra; ss = sp = vpq/N, donde
q = 1 – p. El valor de z viene dado
por

En el caso de que P = X/N, donde
X es el número real de éxitos en una
muestra, z se convierte en

Análogamente pueden obtenerse los resultados para
otros estadísticos.
Curvas
características de operación. Potencia de un
ensayo
Se ha visto cómo el error del Tipo I puede
limitarse eligiendo adecuadamente un nivel de
significación. Es posible evitar el riesgo de error
del Tipo II totalmente, simplemente no aceptando nunca la
hipótesis. Sin embargo, en muchos casos prácticos
esto no puede hacerse. En tales casos, se utilizan a menudo
curvas características de la operación o
curvas OC, que son gráficos que muestran las probabilidades de
errores del Tipo II bajo diferentes hipótesis. Estos
suministran información de cómo en ensayos dados
se logra minimizar los errores del Tipo II, es decir, indican la
potencia de un ensayo para evitar el tomar decisiones
equivocadas. Son útiles en diseño
de experimentos por
mostrar, por ejemplo, qué tamaños de muestras deben
emplearse.
GRAFICOS DE CONTROL
Es a menudo en la práctica importante conocer
cuándo un proceso ha cambiado suficientemente, de modo que
puedan darse los pasos necesarios para remediar la
situación. Tales problemas
aparecen, por ejemplo, en el control de calidad,
donde uno debe, a veces rápidamente, decidir si los
cambios observados se deben simplemente a fluctuaciones
aleatorias o a cambios reales en el proceso de fabricación
a causa de deterioro en las máquinas,
errores de los empleados, etc. Los gráficos de
control suministran un método
útil y sencillo para tratar tales problemas.
Ensayos de
significación en relación con diferencias
muestrales
1. Diferencias de medias
Sean X 1 Y X 2 las medias muestrales
obtenidas en dos muestras grandes de tamaño N 1 Y
N 2 extraídas de poblaciones respectivas que
tienen de media µ1 y µ2 Y
desviaciones típicas s1 Y s2.
Considérese la hipótesis nula de que no hay
diferencia entre las medias poblacionales, es decir,
µ1 = µ2 o que las muestras son
extraídas de dos poblaciones que tienen la misma
media.
Haciendo µ1 = µ2 se ve que
la distribución muestral de la diferencia de medias se
distribuye aproximadamente como una normal con media y
desviación típica dadas por

donde se puede, si es necesario, utilizar las
desviaciones típicas muestrales S1 y S2 como
estimas de s1 y s2.
Con la variable tipificada z que viene dada
por

se puede ensayar la hipótesis nula contra la
hipótesis alternativa (o la significación de una
diferencia observada) a un nivel de significación
apropiado.
2. Diferencias de proporciones
Sean P1 y P2 las proporciones
muestrales de dos grandes muestras de tamaños N1
y N2 extraídas de poblaciones respectivas que
tienen proporciones P1 y P2. Considérese
la hipótesis nula de que no hay diferencia entre
los parámetros poblacionales, es decir, P1 =
P2, Y así las muestras son realmente ex-
traídas de la misma población.
Haciendo P1 = P2 = P, se ve
que la distribución muestral de la diferencia de
proporciones se distribuye aproximadamente como una normal con
media y desviación típica dadas por

donde

se utiliza como una estima de la proporción
poblacional, y q = 1 – p.
Con la variable tipificada z dada
por

se puede ensayar las diferencias observadas a un nivel
de significación apropiado y de este modo ensayar la
hipótesis nula.
Ensayos referentes a otros estadísticos pueden
diseñarse análogamente.
Ensayos
referentes a la distribución binomial
Ensayos que envuelven a la distribución binomial
así como otras distribuciones, pueden diseñar- se
de una manera análoga a los utilizados para la
distribución normal, los principios
básicos son esencialmente los mismos.
Bibliografía
Murray R. Spiegel, Estadística, teoría
y 875 problemas resueltos. Mc Graw Hill, México
1970, pp 167 – 187.
Autor:
Martin del Campo Becerra Gustavo
Daniel
Universidad de Guadalajara
CUCEI
Departamento de
Matemáticas
Elementos de Probabilidad y
Estadística
Maestra: Rosalía Buenrostro
Arceo
Sec. D08
Gustavo Daniel Martín del Campo
Becerra
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |